Data Type
String
startsWith(str): 문자열이 특정 문자로 시작되는지 판별endsWith(str): 문자열이 특정 문자로 끝나는지 판별equal(str): String 문자열 값 비교indexOf(str): 특정 문자열이 대상 문자열의 몇 번째 인덱스에 위치하는지 반환 특정 문자열이 없을 경우에는 -1을 리턴substring: 지정한 범위에 속하는 문자열 반환substring(index): index 위치를 포함하여 이후의 모든 문자열을 리턴substring(beginIndex, endIndex): beginIndex에서 endIndex-1까지의 부분 문자열을 반환replace(beforeStr, afterStr): 특정 문자열을 새로운 문자열로 치환toLowerCase(str): 문자열을 소문자로 변환toUpperCase(str): 문자열을 대문자로 변환trim(str): 문자열의 앞뒤 공백 제거 단, 문자열 내부의 공백은 replace(" ", "")를 사용해야 함charAt(index): 문자열 특정 위치에 있는 문자 반환 인덱스 값으로 마이너스 값을 대입하거나, 문자열 길이보다 큰 인덱스 값을 대입하면 java.lang.StringIndexOutOfBoundsException 오류 발생String.valueOf(str): 지정된 값을 String으로 변환contains(str): 특정 문자열이 포함되어 있는지 확인split(regex): 문자열을 특정 문자열을 기준으로 나는 후 배열을 반환length: 문자열의 길이를 반환
Arrays
Arrays.sort(): 오름차순으로 정렬
기본 정렬 조건이 오름차순인 이유는 Class 내에 기본적으로 구현되어있는
ComparableInterface의compareTo메서드를 기준으로 하기 때문이다. Java에서 인스턴스를 서로 비교하는 클래스들은 모두Comparable인터페이스가 구현되어 있다.
-
정렬 대상 범위를 지정
int[] intArr = new int[] {1, 3, 5, 2, 4}; Arrays.sort(intArr, 2, 5); // intArr[2]~intArr[4]의 값만 정렬 -
내림차순으로 정렬
-
Wrapper Class로 된 배열(Reference Type Array)만 가능함
-
이미 정의된 메소드를 활용하여 정렬 가능
Comparator.reverseOrder()Collections.reverseOrder()
Integer[] integerArr = new Integer[] {1,3,5,2,4}; String[] stringArr = new String[] {"A","C","B","E","D"}; Arrays.sort(integerArr, Comparator.reverseOrder()); //내림차순 Arrays.sort(stringArr, Collections.reverseOrder()); //내림차순
-
-
Arrays.asList(arr): 배열을 ArrayList로 변환 -
Arrays.fill(arr, value): 배열을 value 값으로 채움Arrays.fill(arr, start, end, value): 배열의 start부터 end-1까지 value 값으로 채움
-
Arrays.copyOf(arr, size): 배열의 0번째 원소부터 size만큼 복사 (새로운 배열 생성) -
Arrays.copyOfRange(arr, start, size): 배열의 start원소부터 size만큼 복사 (새로운 배열 생성)
문자형 -> 숫자형
-
Integer, Double, Float 형은 각 클래스에 정의된
valueOf()메소드를 통해 변환할 수 있다.Integer.valueOf(str)Double.valueOf(str)Float.valueOf(str)
-
Integer, Long, Short 형은 각 클래스에 정의된
parse{자료형}()메소드를 통해 변환할 수 있다.Integer.parseInt(str)Long.pareLong(str)Short.parseShor(str)
숫자형 -> 문자형
- String 클래스에 정의된
valueOf()메소드를 통해 변환할 수 있다.String.valueOf(number)
- Integer, Double, Float 형은 각 클래스에 정의된
toString()메소드를 통해 변환할 수 있다.Interger.toString(number)Float.toString(number)Double.toString(number)
정수형 <-> 실수형
- 강제 형변환(Casting)을 통해 변환 가능함
(int)number,(double)number,(float)number
Array <-> List
Array와 List는 반복문을 통해 변환할 수 있다. (시간 초과 가능)
(Reference Type) Array -> List
- Arrays.asList(arr)
- 고정 길이(fixed-size)인 원본 배열의 list view를 반환한다.
- 변환된 리스트에 값을 추가하는 것이 불가능하다.
- 원본 배열의 값을 변경하면 리스트 값도 같이 변경된다.
- new ArrayList<>(Arrays.asList(arr))
- list view를 가지고 새로운 리스트 객체를 만든 것이다.
- 리스트에 값을 추가할 수 있다.
- 원본 배열의 값과 동기화하지 않는다.
- [Java 8 이후] Stream 사용하기
- Stream.of(arr).collect(Collectors.toList())
- Stream의 collect() 메소드는 데이터를 원하는 타입으로 변경해준다.
(Primitive Type) Array -> List
-
반복문 사용하기
// int -> List List<Integer> intList = new ArrayList<>(); for (int element: arr) { intList.add(element); } -
Stream 사용하기
// int -> List List<Integer> intList = Arrays.stream(arr) .boxed() .collect(Collectors.toList());- Stream의
boxed()메소드는 Primitive Stream 값을 Wrapper로 바꿔준다. - 이후
collect()메소드를 통해 원하느 타입으로 변경 가능하다.
- Stream의
List -> Array
arrList.toArray(new String[arrList.size()])- 파라미터로 전달 받은 배열 객체의 길이기 원본 리스트보다 작은 경우, 자동으로 원본 리스트의 size 크기로 배열을 만들어준다.
- 원본 리스트의 길이보다 배열의 크기를 더 크게 지정하면, 나머지 인덱스는 null 로 채워진다.
Collection Framework
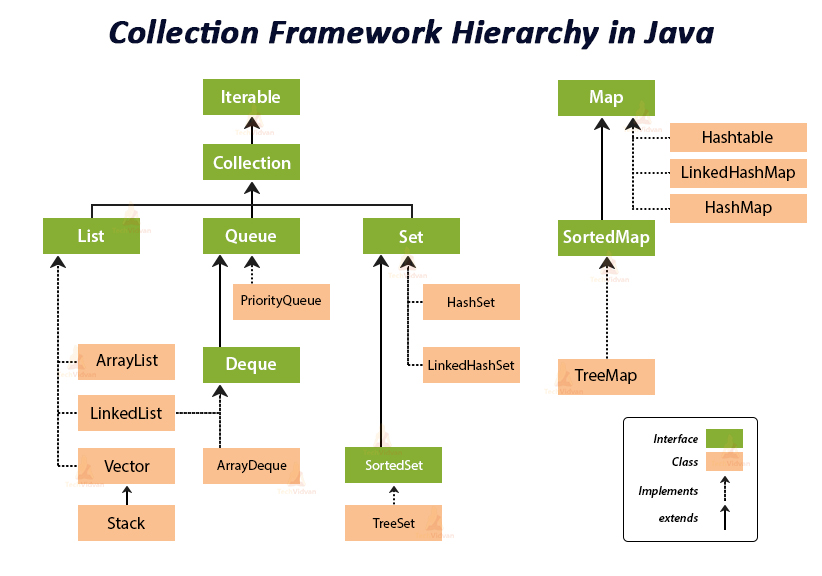
Collections
Collections.sort(c): 컬렉션 객체를 오름차순으로 정렬Collections.max(c): 컬렉션 내의 최댓값 반환Collections.min(c): 컬렉션 내의 최솟값 반환Collections.reverse(c): 컬렉션을 순서를 역으로 변경Collections.copy(fromObj, toObj): fromObj의 모든 객체를 toOBj으로 복사해 반환Collections.bianrySearch(c, obj): 정렬된 컬렉션에서 이진 탐색으로 특정 객체를 찾아 인덱스를 반환Collections.disjoint(c1, c2): 주어진 두 컬렉션에 일치하는 값이 하나도 없으면 true, 하나라도 있으면 false 반환 (= 서로소 집합)
Iterator
Collection 인터페이스에서는 Iterator 인스턴스를 반환하는
iterator()메소드를 정의하여 각 요소에 접근하도록 하고 있다. 따라서 Collection 인터페이스를 상속 받는 List와 Set 인터페이스에서도iterator()메소드를 사용할 수 있다.
hasNext(): 해당 iteration이 다음 요소를 가지고 있으면 true를 반환하고, 더 이상 다음 요소를 가지고 있지 않으면 false를 반환함next(): iteration의 다음 요솔르 반환함
Collection 인터페이스 공통
equals(c): 해당 컬렉션과 전달된 객체가 같은지 확인isEmpty(): 해당 컬렉션 객체가 비어있는지 확인size(): 해당 컬렉션 객체의 크기 반환iterator(): 해당 컬렉션의 반복자(iterator)를 반환toArray(c): 해당 컬렉션의 모든 요소를 Object 타입의 배열로 반환
List
List 인터페이스를 구현한 ArrayList를 주로 사용함
add: 특정 값 추가add(obj): 리스트 끝에 원소 추가add(index, obj): 특정 인덱스에 원소 추가
addAll: 주어진 컬렉션의 모든 객체를 추가addAll(c): 주어진 컬렉션의 모든 객체를 끝에 추가addAll(index, c): 주어진 컬렉션의 모든 객체를 index 위치에 추가
get(index): 특정 인덱스 값 조회set(index, obj): 특정 위치에 객체 저장remove: 특정 값 삭제remove(index): 인덱스에 위치하는 값 삭제remove(obj): 특정 객체 삭제
indexOf(obj): 리스트에서 특정 객체의 인덱스를 반환subList(fromIndex, toIndex): fromIndex와 toIndex-1까지의 부분 리스트 반환contains(obj): 특정 원소가 리스트 내에 있는 지 확인sort(): 리스트를 오름차순으로 정렬sort(comparator): 리스트를 특정 정렬 기준으로 정렬
toArray(): 리스트를 고정 크기의 배열로 전환
Map
Map 인터페이스를 구현한 HashMap을 주로 사용
put(key, value): 맵에 key와 value 값 추가putAll(map): map의 모든 원소를 추가get(key): key와 매핑된 value 반환- 만약 key 값이 없을 땐, null을 반환
remove(key): 특정 key에 해당하는 값을 삭제replace(key, value): 특정 key에 해당하는 값을 value로 대체clear(): 맵에 저장된 모든 객체 제거containsKey(key): 특정 key가 맵에 있는지 판별containsValue(value): 특정 value가 맵에 있는지 판별keySet(): 맵의 모든 key가 저장된 Set을 반환entrySet(): 맵의 모든 entry(=key와 value의 결합) 저장된 Set을 반환values(): 맵의 모든 value 값을 컬랙션 형태로 반환
Set
Set 인터페이스를 구현한 HashSet을 주로 사용
clear(): Set에 저장된 모든 객체 제거getOrDefault(key, defaultValue): key가 없다면 defaultValue로 초기화하여 반환하고, 있다면 해당 key의 value를 반환
아래 함수들은 확인/성공 여부를 boolean 값으로 반환함
add(obj): Set에 특정 요소 추가addAll(c): 주어진 컬렉션의 모든 객체를 집합에 추가 (=합집합)remove(obj): Set에 특정 요소 삭제removeAll(c): 주어진 컬렉션의 객체와 같은 원소를 제거(=차집합)contains(obj): 특정 객체를 포함하는지 확인containsAll(c): 주어진 컬렉션의 모든 객체를 포함하는지 확인(=부분집합)retainAll(c): 주어진 컬렉션의 객체와 동일한 것만 남기고 삭제(=교집합)
Stack
push(obj): 스택의 top에 값을 삽입pop(): 스택의 top 값을 반환한 뒤에 삭제peek(): 스택의 top 값 조회clear(): 스택의 값을 모두 제거empty(): 스택이 비어있는지 확인contains(obj): 스택이 특정 원소를 포함하고 있는지 확인search(obj): 스택에서 특정 원소를 찾아 위치(1부터 시작)를 반환- 원소가 스택에 없다면 -1을 반환
Queue
일반적인 Queue는 LinkedList를 사용함
add(obj): LinkedList 의 마지막에 객체를 추가offer(obj): 큐의 마지막에 객체를 추가- 큐의 크기가 꽉 찼을 경우에 add는 예외를 발생시키지만 offer는 false를 반환
offerFirst(obj): LinkedList의 맨 앞에 객체를 추가offerLast(obj): LinkedList의 맨 마지막에 객체를 추가
poll(): 큐의 맨 앞에 위치한 값을 반환한 뒤에 삭제pollFirst(): LinkedList의 첫번째 노드르 반환하면서 제거pollLast(): LinkedList의 마지막 노드르 반환하면서 제거
peek(): 큐의 맨 앞에 위치한 값을 반환peekFirst(): LinkedList의 첫번째 노드를 반환peekLast(): LinkedList의 마지막노드를 반환
우선순위 큐는 주로 PriorityQueue를 사용
- LinkedList로 구현하는 큐와 사용하는 메소드가 거의 유사
Math
Math.max(n1, n2): 두 인자 중 더 큰 값을 반환Math.min(n1, n2): 두 인자 중 더 작은 값을 반환Math.abs(n): 절댓값을 반환Math.pow(base, exponent): 제곱 값을 반환- 앞의 인자는 밑, 뒤의 인자는 지수를 뜻함
Math.sqrt(n): 제곱근 반환Math.round(n): 소숫점 첫번째 자리에서 반올림한 결과 반환Math.floor(n): 내림 연산 결과 반환Math.ceil(n): 올림 연산 결과 반환
정렬
객체 정렬은 Comparable, Comparator 인터페이스를 적용해 구현할 수 있다.
두 인터페이스는 객체를 비교한다는 점은 같지만, 어떤 대상을 비교하는지가 다르다.
byte, char, double, short, long, int, float 와 같은 Primitive Type 배열에는 적용이 불가능하기 때문에, Wrapper Class를 이용해야 한다.
Comparable의 compareTo(o)
Comparable의 compareTo 메서드는 자기 자신과 매개변수 객체(o)를 비교한다.
public class ComparableExample implements Comparable<Type> {
@Override
public int compareTo(Type o) {
return this.member - o.member; // 정렬 기준이 되는 맴버 변수 지정
}
}
- 정렬 수행 시 기본적으로 적용되는 정렬 기준을 만들기 위해, Comparable 인터페이스를 상속하여 compareTo 메서드를 Override 한다.
- 따라서 정렬 함수를 사용하면 커스텀 기준으로 정렬된다.
Arrays.sort(array)Collections.sort(list)
Comparator의 compare(o1, o2)
Comparator의 compare 메서드는 두 매개변수 객체(o1과 o2)를 비교한다.
public class ComparatorExample {
public static void main(String[] args) {
// 익명 Comparator 객체 구현
public static Comparator<Type> comparator1 = new Comparator<Type>() {
@Override
public int compare(Type o1, Type o2) {
return o1.member - o2.member; // 정렬 기준이 되는 맴버 변수 지정
}
}
}
- 보통 기본 정렬 기준과 다르게 정렬하고 싶을 때, Comparator 익명 클래스(객체) 사용한다.
- 익명 클래스는 특정 타입이 존재하는 것이 아니기 때문에, 반드시 구현(상속)할 대상이 있어야 한다.
- 정렬 함수의 두 번째 인짜로 Comparator 객체를 넣어 정렬 기준을 정할 수 있다.
Arrays.sort(array, myComparator)Collections.sort(list, myComparator)
compare(o1), compareTo(o1, o2)의 동작 원리
반환값이 0 또는 음수이면 자리가 그대로 유지되며, 양수인 경우에는 두 객체의 자리가 바뀐다.
- 오름차순으로 정렬하고 싶으면, 아래와 같이 구현한다. (내림차순은 반대로 한다.)
현재 객체<파라미터로 넘어온 객체→ 음수 리턴현재 객체==파라미터로 넘어온 객체→ 0 리턴현재 객체>파라미터로 넘어온 객체→ 양수 리턴
- 좀 더 간단하게 객체 간의 뺄셈으로도 구현할 수 있다. 하지만, 연산 결과가 객체 타입의 유효 범위를 넘어서는 Underflow, Overflow가 발생할 수 있으니 주의하자.
현재 객체-파라미터로 넘어온 객체
순열과 조합
순열(Permutation)
nPr의 의미는 n개의 숫자에서 r개를 뽑아 정렬하는 가짓수이다.
순열은 중복을 허락하지 않기 때문에, visited 배열을 통해 방문 여부를 확인한다.
/*
순열 구현 코드
- r: 뽑고자 하는 개수
- temp: r개를 뽑은 결과값을 저장해놓은 배열
- current: 현재 개수를 저장해 놓는 값
- visited: 방문 여부를 확인하는 배열
*/
public static void makePermutation(int r, int[] temp, int current, boolean[] visited){
if(r == current){
// r개의 수를 선택했다면 출력
System.out.println(Arrays.toString(temp));
}else{
for(int i = 0; i < arr.length; i++){
if(!visited[i]){
visited[i] = true; // 아직 방문하지 않았다면 방문 처리
temp[current] = arr[i]; // 방문한 숫자를 결과에 추가
makePermutation(r, temp, current + 1, visited); // 다음에 방문할 숫자 탐색
visited[i] = false; // 방문 처리 해제
}
}
}
}
makePermutation 함수는 재귀적으로 동작하며, 1개의 숫자를 뽑아 방문 처리를 한 후 결과 리스트에 추가하는 과정을 반복한다.
- 배열을 반복하며, 방문하지 않았다면 방문 처리를 한다.
- 방문한 숫자를 결과 리스트에 추가한다.
- 다음 숫자를 뽑기 위해
makePermutation을 호출한다. - 방문 처리를 해제하여 다음 경우의 수를 만들 수 있게 한다.
- 원하는 숫자 개수만큼 뽑았다면, 이때 결과 리스트를 반환한다.
조합(Combination)
nCr의 의미는 n개의 숫자에서 r개를 뽑는 경우의 수이다.
조합에서는 순서가 중요하지 않기 때문에 visited 배열이 필요하지 않다. 하지만 이미 선택한 숫자는 선택하지 않기 때문에, 다음 숫자를 start 인덱스를 계속 증가시키며 start 이후의 값들 중에서 뽑을 수 있도록 범위를 제한한다.
/*
조합 구현 코드
- r: 뽑고자 하는 개수
- temp: r개를 뽑은 결과값을 저장해놓은 배열
- current: 현재 개수를 저장해 놓는 값
- start: 그 다음 반복문을 시작하는 값
*/
public static void makeCombination(int r, int[] temp, int current, int start){
if(r == current){
// r개의 수를 선택했다면 출력
System.out.println(Arrays.toString(temp));
}else{
for (int i = start; i < arr.length; i++){ // 이미 선택한 대상을 제외하기 위해 start 인덱스 부터 순회
temp[current] = arr[i];
makeCombination(r, temp, current + 1, i + 1);
}
}
}
makeCombination 함수는 재귀적으로 동작하며, start 인덱스 이후의 범위에서 1개의 숫자를 뽑아 결과 리스트에 추가하는 과정을 반복한다. start 인덱스는 이미 뽑은 값을 제외하기 위해 계속 증가한다.
- 배열을 start 인덱스부터 반복하며, 아직 선택하지 않은 숫자들을 반복한다.
- 선택하지 않은 숫자 중 하나를 뽑아 결과 리스트에 추가한다.
- 다음 숫자를 뽑기 위해
makeCombination을 호출한다.
- 원하는 숫자 개수만큼 뽑았다면, 결과 리스트를 반환한다.
중복 순열
중복 순열은 숫자가 중복되어도 되기 때문에 visited 배열이 필요 없다.
/*
중복순열 소스코드
- r: 뽑고자 하는 개수
- temp: r개를 뽑은 결과값을 저장해놓은 배열
- current: 현재 개수를 저장해 놓는 값
*/
public static void makeOverlapPermutation(int r, int[] temp, int current){
if(r == current){
System.out.println(Arrays.toString(temp));
}else{
for(int i = 0; i < arr.length; i++){
// 중복 순열은 숫자가 중복되어도 되기 때문에 visited 배열이 필요 없다
temp[current] = arr[i];
makeOverlapPermutation(r, temp, current + 1);
}
}
}
중복 조합
중복 조합이므로 현재 선택한 값이 또 나올 수 있게 start 인덱스를 유지한다.
/*
중복조합 소스코드
- r: 뽑고자 하는 개수
- temp: r개를 뽑은 결과값을 저장해놓은 배열
- current: 현재 개수를 저장해 놓는 값
- start: 그 다음 반복문을 시작하는 값
*/
public static void makeOverlapCombination(int r, int[] temp, int current, int start){
if(r == current){
System.out.println(Arrays.toString(temp));
}else{
for(int i = start; i < arr.length; i++){
temp[current] = arr[i];
makeOverlapCombination(r, temp, current + 1, i); // 중복 조합이므로 현재 선택한 값이 또 나올 수 있게 start 인덱스를 유지
}
}
}
BFS/DFS
BFS와 DFS는 그래프를 탐색하는 방법 중 하나로 탐색 시 어떤 노드(정점)를 우선적으로 방문하느냐에 따라 나뉜다.
- 두 방법 모두 이미 방문한 노드는 방문하지 않기 위해, visited 배열을 통해 방문 여부를 확인한다.
- [선 방문 확인] 아직 방문하지 않은 노드의 인접 노드들을 방문한다.
- [후 방문 확인] 인접 노드들 중 방문하지 않은 노드를 방문한다.
BFS(Breadth First Search)
!https://media.vlpt.us/images/lucky-korma/post/2112183b-bfcd-427e-8072-c9dc983180ba/R1280x0-2.gif
- 시작 노드로부터 가까운 노드를 먼저 방문하고, 멀리 떨어진 노드를 나중에 방문하는 방법이다.
- 주로 두 노드 사이의 최단 경로를 찾고 싶을 때 사용한다.
- 가까운 노드부터 방문하는 BFS의 특성상, 목적지 노드에 도착했을 때 최소 거리라는 것을 보장할 수 있기 때문이다.
BFS 구현
BFS는 큐를 이용해 구현한다.
public static boolean[] visited = new boolean[9];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// BFS 함수 정의
public static void bfs(int start){
Queue<Integer> q = new LinkedList<>();
q.offer(start);
// 현재 노드를 방문처리
visited[start] = true;
// 큐가 빌때까지 반복
while(!q.isEmpty()){
// 큐에서 하나의 원소를 뽑아 출력
int x = q.poll();
System.out.println(x + " ");
// 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for(int i = 0; i < graph.get(x).size(); i++){
int y = graph.get(x).get(i);
if(!visited[y]){
q.offer(y);
visited[y] = true;
}
}
}
}
- 시작 노드를 큐에 삽입(
offer)하고 방문 처리를 한다. - 큐가 빌 때까지 아래 시퀀스를 반복한다.
- 큐에서 노드 하나를 꺼낸다. (
poll) → 이때 큐에서 노드를 꺼낸 순서가 BFS 탐색 순서이다. - 해당 노드와 인접한 노드들 중, 아직 방문하지 않은 노드를 큐에 삽입(
offer)하고 방문 처리를 한다.
- 큐에서 노드 하나를 꺼낸다. (
DFS(Depth First Search)
!https://media.vlpt.us/images/lucky-korma/post/30737a15-9adf-49a6-96a0-98c211cab1cc/R1280x0.gif
- 시작 노드에서 한 분기를 완벽하게 탐색한 후, 다음 분기를 탐색하는 방법이다.
- 모든 노드를 방문하고자 하는 경우, 주로 이 방법을 사용한다.
DFS 구현
DFS는 재귀함수와 스택을 이용해 구현한다.
public static boolean[] visited = new boolean[9];
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// DFS 함수 정의
public static void dfs(int x){ // x: 노드 번호
// 현재 노드를 방문 처리
visited[x] = true;
System.out.println(x + " ");
// 현재 노드와 연결된 다른 노드를 재귀적으로 방문
for(int i = 0; i < graph.get(x).size(); i++){
int y = graph.get(x).get(i);
if(!visited[y]) dfs(y);
}
}
- 시작 노드를
dfs함수에 전달하여, 다음 시퀀스를 반복한다.- 현재 노드를 방문 처리한다. → 이때 방문한 노드 순서가 DFS 탐색 순서이다.
- 현재 노드의 인접 노드들 중 아직 방문하지 않은 노드에 대해
dfs를 재귀적으로 호출한다.
BFS / DFS 문제 유형
- 그래프의 모든 정점을 방문하는 것이 중요한 문제 → DFS/BFS
- DFS/BFS 모두 모든 정점을 방문할 수 있기 때문에 둘 다 사용가능하다.
- 일반적으로 DFS의 구현이 더 간단하기 때문에, DFS를 많이 사용하기도 한다.
- 경로의 특징을 저장해야 하는 문제 → DFS
- 경로의 특징 = ‘경로에 같은 숫자가 있어서는 안된다’는 등의 제한조건
- BFS는 한 경로를 한번에 탐색하지 않고, 여러 경로를 번갈아 가면서 탐색하기 때문에 경로의 특징을 저장할 수 없다.
- 최단 거리를 구해야 하는 문제 → BFS
- BFS는 가까운 노드들부터 탐색하기 때문에, 목표 노드를 만났을 때 거리가 최소라는 것을 보장할 수 있다.
이진 탐색
이진 탐색은 정렬된 리스트에서 원하는 값을 고속으로 탐색하는 방법이다.
- 이진 탐색은 핵심은 매 반복마다 탐색 범위를 반으로 줄이는 것이다.
- 정렬된 리스트의 중앙값을 조사하여, 찾는 값이 왼쪽 리스트 혹은 오른쪽 리스트에 속하는지 확인한다.
- 찾는 값이 속하지 않은 쪽의 리스트는 다음 탐색 범위에서 제외한다.
- 이 경우 시간 복잡도는 이진 트리의 높이인
*O(logn)**과 같다고 볼 수 있다.
이진 탐색(Binary Search)
리스트에 특정 값이 있는지 빠르게 확인하는 방법이다.
- 이진 탐색은 탐색 범위의 시작점(
start)과 끝점(end)가 만나지 않는 동안, 탐색 범위를 반으로 줄이는 과정을 반복한다.
이진 탐색 구현 - 재귀함수
- 시작점(
start)이 끝점(end)보다 크면 종료한다.
// 이진 탐색 소스코드 구현(재귀함수)
public static int binarySearch(int[] arr, int target, int start, int end){
if(start > end) return -1;
int mid = (start + end) / 2;
if(arr[mid] == target){
// 찾은 경우 중간점 인덱스 반환
return mid;
}else if(arr[mid] > target){
// 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
return binarySearch(arr, target, start, mid-1);
}else{
// 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
return binarySearch(arr, target, mid+1, end);
}
}
이진 탐색 구현 - 반복
- 시작점(
start)이 끝점(end)보다 작거나 같은 동안 반복한다.
// 이진 탐색 소스코드 구현(반복문)
public static int binarySearch(int[] arr, int target, int start, int end){
while(start <= end){
int mid = (start + end) / 2;
if(arr[mid] == target){
// 찾은 경우 중간점 인덱스 반환
return mid;
}else if(arr[mid] > target){
// 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
end = mid - 1;
}else{
// 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
start = mid + 1;
}
}
return -1;
}
이진 탐색 구현 - Arrays.binarySearch()
- 단순히 배열에서 해당 값의 위치를 빠르게 찾고 싶다면, 내장함수를 사용한다.
- 검색 성공 시 해당 값의 인덱스를, 검색 실패 시 -1을 반환한다.
int[] arr = {3, 4, 1, 2, 5};
Arrays.sort(arr); // 이진 탐색 전 배열 정렬
int index = Arrays.binarySearch(arr, 4);
파라매트릭 서치(Parametric Search)
이진 탐색의 원리를 이용해 최적화 문제를 결정 문제로 바꾸는 방법이다.
- 최적화 문제 : 어떤 문제의 최적값을 찾는 문제
- 해당 조건을 만족하는 최적값을 찾아라
- 자동차를 탈 수 있는 사람 중 가장 어린 사람을 찾아라
- 결정 문제 : 어떤 문제가 조건에 맞는지 Yes/No로 결정하는 문제
- 정렬된 데이터에서 이 값은 해당 조건을 만족하는가?
- 사람들이 나이순으로 정렬되어 있을 때, 이 사람은 자동차를 탈 수 있는가?
- 파라매트릭 서치는 결정 문제라는 점이 이진 탐색과 다르다.
동적 계획법
동적 계획법은 복잡한 문제를 여러 개의 작은 부분 문제로 나누어 해결하는 방법이다.
- 동적 계획법의 핵심은 Memoization 기법을 사용하는 것이다.
- Memoization은 반복되는 결과를 메모리에 저장해서, 중복 호출 되었을 때 (계산을 반복하지 않고) 재사용 하는 기법이다.
- 즉, 부분 문제의 결과를 저장하여 큰 문제를 풀 때 사용하는 것이다.
DP 구현 - Top-Down
- Top-Down은 큰 문제(Main Problem)에서 작은 부분 문제(Sub Problem)를 재귀적으로 호출하여 리턴된 값으로 문제를 해결하는 방법이다.
// 한 번 계산된 결과를 메모이제이션(Memoization)하기 위한 배열 초기화
public static long[] d = new long[100];
// 피보나치 함수(Fibonacci Function)를 재귀함수로 구현 (탑다운 다이나믹 프로그래밍)
public static long fibo(int x) {
// 종료 조건(1 혹은 2일 때 1을 반환)
if (x == 1 || x == 2) {
return 1;
}
// 이미 계산한 적 있는 문제라면 그대로 반환
if (d[x] != 0) {
return d[x];
}
// 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
d[x] = fibo(x - 1) + fibo(x - 2);
return d[x];
}
DP 구현 - Bottom-Up
- Bottom-Up은 작은 부분 문제(Sub Problem)를 미리 계산해 배열에 저장해두고, 이 값들을 모아 큰 문제를 해결하는 방식이다.
public static void fibo(){
public static long[] d = new long[100];
// 첫번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1;
d[2] = 1;
int n = 50; // 50번째 피보나치 수를 계산
// 피보나치 함수(Fibonnacci Function) 반복문으로 구현(보텀업 다이나믹 프로그래밍)
for (int i = 3; i <= n; i++){
d[i] = d[i-1] + d[i-2];
}
}
DP 문제 유형
DP 문제 판별
아래 두 가지 조건을 만족하는 문제는 DP를 이용해 해결할 수 있다.
- 최적 부분 구조 : 큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아 큰 문제를 해결할 수 있다.
- 중복되는 부분 문제 : 동일하게 반복되는 작은 문제로 해결해야 한다.
대표적인 DP 문제
- Coin Change Problem (동전 교환 문제)
- KnapSack Problem (배낭 문제)
- LCS (Longest Common Subsequence, 최장 공통 부분 수열)
- LIS (Longest Increasing Subsequence, 최장 증가 부분 수열)
- Edit Distance (편집 거리)
- Matrix Chain Multiplication (행렬 곱셈 문제)

